Habitat Modeling - Part 2: Model Evaluation

So far, we've run two habitat analyses for our pigmy salamander. The first was a rule-based analysis in which we applied expert knowledge to identify a set of pixels that meet the requirements of "habitat" for the pigmy salamander. In the other, we used maximum entropy, a model which uses species presence data to identify patterns in the distribution of values pulled from environmental layers at these locations to assign a score to each pixel that reflects the likelihood that that pixel is habitat.

In this continuation of the habitat modeling exercise we examine our modeling results. First, we examine ways the various models can be tuned and validated. Did we perhaps include too much habitat in our result? Too little? How can we tell? And second, we step back and look not at how well our model might have performed, but instead focus in on where the model did not perform well. Why might we see a salamander in a place where we did not expect based on our model? Or conversely, why are there no salamanders in a place where there is perfectly good habitat?

Your final assignment for this exercise (parts I and II) will be to write a brief report on your habitat models for the pigmy salamander. Components of the report are outlined in the "Deliverables" section at the end of this document.

Objective 1: Model Tuning

Ultimately, we want to produce a map that shows where pigmy salamander habitat is and is not, i.e.. a binary map with one value for habitat and another value for non-habitat. The rule based approach generates this automatically. However, for the MaxEnt product (as well as many other statistics-based models), we must select a probability threshold above which we classify as habitat and below which call non-habitat. Choosing what threshold to use is not an arbitrary process: if we choose a low threshold then we are likely to include places in our habitat map that aren't really suitable for salamanders; but if we chose a high threshold then we are likely omitting areas that are perfectly fine four our salamanders.

Deciding on a threshold, often termed as model tuning, is the first objective of this exercise. Tuning a model requires species presence data and ideally species absence data. However, as true absence data are usually not available, we create pseudo-absence data which are simply a random grab of points within the extent of our analysis that we assume do not fall in habitat. With presence and absence data and a modeled habitat map, we can evaluate our map by generating a confusion matrix. To do this we simply overlay our known salamander occurrences and [pseudo]absences on top of our predicted habitat map to categorize each point into one of four categories: true positive (a recorded occurrence falls on a predicted habitat cell), false positive (recorded [pseudo]absence falls on a predicted habitat cell), true negative (recorded [pseudo]absence does not fall on a predicted habitat cell), and a false negative, (recorded presence does not fall on a predicted habitat cell). [It may help to remember that the true and false refer to whether the prediction was accurate or not...]

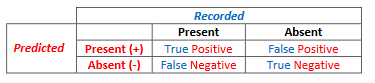
Each probability threshold selected will have a potentially different set of confusion matrix values since the area of predicted habitat changes with a given threshold value. Tuning a model refers to changing the threshold and seeing how it effects these numbers.

A model can be tuned to ensure that all observed presence points fall within predicted habitat by lowering the probability threshold for classifying a pixel as habitat. Set the threshold to zero and the entire landscape becomes classified as habitat and all your positives (recorded presences) will be true positives. This is termed a maximally sensitive model, since the model is sensitive to all possible species presences and will include them in the result.

Of course, increasing a model's sensitivity will also increase your false positive rate (i.e. classifying habitat where there aren't really any individuals). If you want to avoid false positives, you'd increase your probability threshold so that only the cells most resembling habitat in your model get classified as habitat. This is referred to as increasing your models specificity as the predicted habitat is a much more specific portion of the landscape. Of course, increasing a model's specificity will increase the rate of false negatives, that is, of excluding actual habitat areas in your modeled result.

One goal of model tuning is to find a balance between model sensitivity and model specificity. This is often using the Receiver Operating Characteristic or ROC curve approach. These curves are developed by generating the confusion matrices for a sequence of probability thresholds and then plotting the rate of true positives to the rate of false positives for each of the probability thresholds. If the model was poor, in which case habitat pixels were scattered randomly across [geographic and parameter] space, you'd get a steady increase of both false positives and true positives as you lowered your probability threshold (and classified more landscape as habitat). If your model was successful in discriminating habitat from non-habitat, the rate of true positives would increase much more quickly than the rate of false positives as you lowered your threshold and you'd see a large arc deviating away from the line generated from a "random guess". The probability threshold at which the curve deviates most from the "guessing line" represents the best balance between model specificity and sensitivity.

The steps below outline the procedure for generating pseudo-absence points and creating a confusion matrix for the threshold we chose based on the MaxEnt analysis. These steps are also quite useful for analyzing other statistics-based model output (e.g. GLM, GAMs).

Step 1a. Creating a pseudo-absence points

Follow these steps to create a point feature class (called Samples.shp) which includes our known salamander locations and a set of locations we are assuming the salamanders do not exist [pseudo-absences].

• Create a new geoprocessing model (e.g. "Create pseudo absence points")
• Add the Create Random Points tool. Set it to create random points within the extent of the salamander observation points shapefile (PigmySalamanders_South.shp) and to create the same number of absence points as the salamander observations. Finally, set the points to be created at least 500 m from each other so that the points aren't clustered. Name the output Sample.shp in your data folder.
• Add the Append tool to your model and use it to append the salamander observation points to your newly created random points. Note: as the two datasets have different attribute table structures, or schema, you'll have to adjust the Schema Type setting in the Append tool...
• Make a feature layer from the Append tool output. We need to do this so we can select a subset of features in the next step.
• Use the Select Layer by Location tool to select all the points in the layer file created above that intersect the salamander observation points.
• Add the Calculate Field tool to set the ID values of all the selected records (i.e. those that represent salamander presence locations) to 1.

Add the result to your map and symbolize the data so that the different ID values are different symbols. The 1's represent observed salamander presence and the others are your pseudo-absence points. We can use these locations as samples to generate a confusion matrix.

Step 1b. Generating a confusion matrix from sample points

Now that we have our known salamander presence and [pseudo]absence locations, we can evaluate how well our model did in terms of sensitivity and specificity. The point shape file we just created above represents our observations, and what we need to do now is link our predictions with these observations, and with that we can tally our true positives/negatives and our false positives/negatives...

• Create a new geoprocessing model (e.g. "Create confusion matrix").

• Add the Extract Values to Points tool and use it to extract the values from your MaxEnt habitat probability map (the continuous, not the binary one) for the locations of your presence/absence points created in the previous step.

• Add the result to your map and look at the attribute values. The field Id remains from your previous step; here a 1 is an observed presence and a 0 is a [pseudo]absence. The new field (RASTERVALU) lists the Maxent predicted habitat likelihood at that location.

• Either in your model or manually, a third column named Predicted to this attribute table and compute all values below your MaxEnt "Balance training omission, predicted area and threshold value" to zero and those above to 1 (just as we did to produce the binary raster).

  → TIP: You can use the calculator expression: [RASTERVALU] > 0.028) to assign 1's and 0s (replacing 0.028 with the threshold you got...)

• Sort this table on the RASTERVALU attribute. If your MaxEnt model were absolutely correct, you would see all zeros in the Id column (i.e. observed presence/absence) sort perfectly with the crossover between zeros and ones occurring right at your chosen threshold. However, chances are that you don't see this; instead we see classification errors.

• Add the Summary Statistics tool to your model; we'll use this to summarize the results above into a table listing how many points fall into each of the four confusion matrix sectors. Set the Statistics field to be the COUNT of the ID (or any other) field. For the case field, select both the Id and Predicted fields.

• View the output of the Summary Statistics tool. It's not the same format as the confusion matrices discussed above or in class, but the information is there.

  • The row with an ID value = 1 and a Predicted = 1 are the true positives. (Habitat was predicted where we observed the species.)
  • The row with an ID value = 0 and a Predicted = 1 are the false positives. (The observed absence point was found within predicted habitat.)
  • The row with an ID value = 0 and a Predicted = 0 (or -9999) are the true negatives (The observed absence point was located outside of predicted habitat.)
  • The row with an ID value = 1 and a Predicted = 0 (or -9999) are the false negatives (The observed presence was found outside of predicted habitat.)

  Note that you may not actually get values for all 4 categories; MaxEnt tends to predict high habitat likelihoods where supplied presence points occur, causing false negatives to be very infrequent. If you have a large number of presence records, you should omit a few in creating your MaxEnt model and reserve them to use here to get a more reliable show of false negatives.

Confusion matrices give us a useful indication of how sensitive or specific a particular threshold is and how well the model works. You can calculate the "percent true" by summing the "true" occurrences (true positives and true negatives) and dividing that sum by the total number of presence/absence points used in creating the confusion matrix. Related to this, but slightly more complex is the kappa statistic. (See a statistics text book or this link to find how it's calculated). A higher kappa statistic reflects better agreement between what's observed and what's predicted, i.e. a better model.

However, it's often the AUC or "Area Under the [ROC] Curve" that's used to assess the overall quality of a habitat model. Determining the AUC begins with developing the ROC curve, which as described above, is a matter of plotting true positives against true negatives for a series of probability thresholds. The AUC is simply the area between that curve and the guessing line. A higher value indicates a better model.

Several statistics packages can calculate ROC and AUC for a set of presence/absence points tagged with modeled habitat likelihood values. ("ROCR" is one that is popular in 'R'.) It's therefore overkill to try this in ArcGIS (though you could do it through repeating the steps above...). However, it may be useful, depending on your overall objective, to calculate the confusion matrices from a range of probability thresholds, i.e., ones that reflect conservative or liberal interpretations of your habitat likelihood values.

Before moving on, it is important to note that confusion matrices should ideally be created with a data set that is independent from the presence and [pseudo]absence points used to develop the model.] Collecting presence and absence data, however, is a challenging task and more often than not (particularly for rare and/or endangered species) these data are quite sparse. Consequently, it's quite common, though still discouraged, to use the same dataset for both. There are statistical implications for this -- as well as methods to overcome these implications; if you do not understand these fully yourself, you should consult a statistician.

Objective 2: Model Interpretation

Model tuning allows us to tweak probability thresholds so that we may generate binary habitat maps from a probability surface that reflect various priorities (increased sensitivity, specificity or a balance of the two). The confusion matrices developed by overlaying known presence and absence data on top of binary prediction models also provide a means for validating our model. You could stop there -- with a binary map showing where you are likely to find the species along with some measure of how confident you are in that prediction, but if you did you'd be overlooking some potentially useful and interesting findings...

Turns out that habitat maps derived from models are rarely, if ever, perfect, but their imperfections can sometimes reveal new aspects about the species and its distribution. The second objective of this part of the lab assignment is therefore to explore a few methods for critically reviewing our habitat models, particularly where they go "wrong", and assessing them from a more informed ecological perspective.

We should be clear, however, that interpreting models is not an entirely straightforward process. In fact, it may be considered more "art" than science, and certainly it is influenced by how much information is at your disposal and how familiar you are with the local landscape and the species in general. Often, it really boils down to looking at the results from a human perspective to identify patterns that the computer was not (or could not have been) taught. And in this light, GIS becomes a huge asset in exploring the results, both visually and analytically.

That said, we will explore some spatial analysis techniques to explore points in our presence/absence dataset that fall "off the diagonal" in the confusion matrix, i.e. the false positives and false negatives. We also revisit our rule-based analysis and examine a few simple ways we can dissect that product to reveal patterns that underlie its result.

Step 2a. Distance to habitat.

It's possible that a species observation does not land in what we ultimately classify as habitat because our model just got it wrong. However, it's also possible that the observer spotted the individual outside its habitat for a valid, explainable reason. It could be that, because of some population pressure or competition, that a salamander decided that marginal habitat offered a better chance at success than optimal habitat for whatever reason. (Ask a metapopulation scientists for more info on this....)

To explore whether this might be the case, we can calculate distance from habitat and identify how far away from suitable habitat this false negative was. (Again, however, you're not likely to have many false negatives in the MaxEnt result.) The assumption is that, if a species was observed close to habitat, it's more plausible that the individual may have been found wandering outside its niche. We can easily calculate this with GIS

• If you don't already have a habitat/NoData map derived from the rule based result, create one.
• Calculate Euclidean distance from habitat.
• Use the Extract Values to Points to tag each Sample Point (the ones generated in step 1b with the prediction values as well as the recorded values) with its distance from habitat.
• Examine the attribute table for the result. False negatives will show up as records with an Id value = 1 and a RASTERVALU > 0. How far are your false negatives (if any) from classified habitat?

Step 2b. Examining Rule Based Analyses

Our rule based model appears to give us a fairly opaque result. We could potentially build a confusion matrix from the model output, but since rule-based models are frequently based on the premise that we don't have accurate presence/absence data, this is usually impossible. Instead, interpretation of rule based analyses is often done by visual inspection of someone knowledgeable of the species and the terrain, i.e. an Expert - perhaps the same expert or experts that provided the advice on the model.

GIS is a natural ally in this post-hoc analysis in that it allows easy visualization of the model in the context of other layers that may be available. However, there are additional steps that can provide useful introspection into the rule based analysis. One simple method is to examine the components of the rule individually to see which ones appear the most limiting. For example, perhaps we have a case where a simple elevation constraint explains 90% of the habitat selected, with the additional 10% resulting from pixels not meeting the other variables.

To explore these relationships, we can tweak our existing rule-based geoprocessing model to show much more information. Use these steps to guide you.

• Create a new geoprocessing model (e.g. "Rule Based Examination")
• Add the four datasets used to create the original rule based model (Elevation, FocalForest400, Mean temperature of the warmest month, Mean precipitation of the driest month).
• Add an instance of Raster Calculator tool. This time, however, add the different criteria together instead of using a logical AND function (though continue to treat the elevation constraint as a single variable, as below).

((Elevation > 760) & (Elevation < 2012)) + (FocalForest400 > 0.5) + (Tmax < 1800) + (PPTdriest > 9600)

View the result. The values, which range from 0 to 4, indicate the number of criteria met. Those with a value of 4 should be the same as those classified as habitat in the rule-based outcome. However, now we are able to see cells that missed being classified by habitat by not meeting one or criteria. Experts may appreciate seeing this to discover places where, if the criteria were relaxed a bit, more places would be considered habitat.

Again, these are just some simple ways to examine the habitat modeling results more carefully and thoughtfully. They may not reveal anything, but you can at least appreciate that there may be more to the story than just producing a habitat map.

Summary

Model tuning and interpretation are an essential component in habitat modeling. The temptation to blindly run rule-based, maximum entropy, or other statistical analysis to generate a binary habitat map and be done with it should be avoided. It is not good science and ignores data that can possibly lead to some new discoveries.

Tuning and interpretation involve looking at your results in both parameter and geographic space. How does changing the probability thresholds affect the distribution of habitat and the rate false positives and false negatives? What if we were spatially extend our found habitat? Would the area subsumed into "habitat" be justified? Why do we find individuals in some habitat areas and not in others?

In the next set of exercises for this class we will build off of a habitat suitability map, examining all the interesting aspects of "habitat" that can be used in prioritizing a landscape for conservation. It's important to keep a critical eye on how errors and misinterpretations of habitat model results can compound as we involve these results in subsequent analyses.

Assignment/Deliverables

You have now completed two habitat models for the pigmy salamander. Your assignment is to compile your methods, analysis, results, and model interpretations into a brief report. Components of this report are outlined below; this is to streamline your write-up so that you can concentrate on the relevant analysis and not worry as much about getting your presentation perfect. Do, however, pay attention to the requirements of each as failure to submit anything asked for will likely lead to a deduction. The report need not follow any strict format other than providing what is requested in an organized fashion. (If in doubt, think of any means possible that will make your grader make grading your assignment more easy. A disorganized submission will certainly make him or her cranky in a hurry...)

Overview

• Begin your report with a brief section (one or two paragraphs) summarizing information on the pigmy salamander that may be relevant for modeling its habitat. While this does not have to be exhaustive for this analysis (the points made in the lab description will suffice), do examine a few of the web sites provided and be sure to cite where the information you mentioned was obtained (a website URL or paper citation is fine).

Environmental layer development

• Distance to streams analysis. Submit a figure of the geoprocessing model used to calculate distance from stream. This does not have to be in color, but make sure it is legible.
• Focal forest maps. Create a 3-panel map showing the GAP cover types used in creating your "focal forest" layers (classes 63, 84, & 96) as well as the 150 m focal forest and the 400 m focal forest results. Points will not be deducted for cartographic details on this figure; I just want to visually inspect that your maps to see they were created correctly. There's no need to add a scale bar, north arrow, legend, etc. Just make sure each map is clearly labeled and clipped to the extent of the study area. Don't spend too much time making this map pretty, and it can be a grayscale map (as long as the maps convey their relevant information).

Rule-based analysis

• Create a grayscale figure displaying your rule-based model result for the study area. This time, be sure to include a scale bar, north arrow, legend, projection information, your name and date in the figure. Also indicate (in words) the criteria used in modeling the habitat and the total area of habitat created, in $km^2$. (Be sure to use meaningful names, not just data names, e.g. "elevation" not "NED30". Include (for reference) the salamander locations on this map and a graticule, if you know how.
• In support of your rule-based analysis, provide a map showing the number of criteria in the rule equations that each pixel in the study area meets. (For example a value of zero indicates that the pixel meets none of the 4 criteria; use the method described in step 2b above to create this map.) Include all the cartographic elements mentioned in the other rule-based map. Also, describe anything you can discern in this map. For example, can you guess which rule layers tend to be filtering out most of the habitat and which seem mostly redundant? What are the relative proportions of pixels meeting 3 criteria to those meeting 4?

MaxEnt analysis

• Create a grayscale figure displaying your MaxEnt derived habitat likelihood result for the study area. Use darker shades to represent higher likelihoods of finding the pigmy salamander. Be sure to include a scale bar, north arrow, legend, projection information, your name and date in the figure.
• Include the MaxEnt jackknife figure with a brief description of what it shows in terms of each different variable's contribution to the gain. What does the jackknife figure tell you about which variables are important to the model?
• Present the dependence response curves (not the marginal ones) for distance to stream, elevation and mean temperature of the coldest month. Describe any patterns you see in each in terms of how each might influence salamander habitat.
• Create a figure displaying your MaxEnt habitat classification map. Include the same cartographic elements as the previous MaxEnt map. Indicate the threshold used and the total area of habitat predicted. Also, include the salamander presence and pseudo absence points on this map; clearly labeling or symbolizing which points are presence and which are absence.
• Generate a confusion matrix from the MaxEnt habitat classification. Describe how you might make your model more sensitive and how this would change the values in your matrix. Repeat for if you made your model more specific.
• Compute a confusion matrix for your rule-based result using the presence/pseudo-absence data you generated in this lab. Create a table of false negatives and their distance to the nearest habitat pixel. Do any misclassified salamander presence points appear close to predicted habitat? What might this suggest?

AFTER YOU ARE FINISHED, PLEASE TAKE A MOMENT TO CLEAN UP YOUR WORKSPACE...

• Delete your National Map, PRISMdata, and SEREgionalGAP folders; these can be extracted from the zip file on Sakai quite easily.
• Delete your ASCII folder containing MaxEnt inputs. This can be recreated easily.
• Clear out your scratch folder
• Delete or zip up your EnvLayers folder .
• Remove any other extraneous files. They should all be easily reproducible with your models.

Model for creating pseudo-absences...

Model for creating a confusion matrix from a habitat probability raster